RC4是美国密码学家Ron Rivest在1987年设计的密钥长度可变的流加密算法。它加解密使用相同的密钥,因此也属于对称加密算法。RC4曾被用在有线等效加密(WEP)中,但由于其错误的使用的方式已被有效破解,而如今,它又被TLS协议所放弃。
在2015年2月发布的RFC7465中,RC4密码套件被禁止在TLS各版本的客户端和服务端使用。客户端禁止在ClientHello中包含RC4套件,服务端禁止从ClientHello中提供的密码套件中选择RC4,如果客户端只提供了RC4,服务端必须终止握手。另外,谷歌、微软、Mozilla也宣布将于明年年初在各自的浏览器中停止对RC4的支持。
从1994年RC4被匿名公开在Cypherpunks邮件列表,到如今RC4被TLS协议放弃,安全研究员们做出了很多贡献。
RC4算法分为两个部分。第一部分是密钥调度算法(key-scheduling algorithm),根据key初始化S盒,第二部分是伪随机数生成算法(Pseudo-random generation algorithm),生成密钥流,同时更新S盒的状态。
密钥调度算法:
Input: 密钥K ,K长度L字节
Output:初始化后的S盒子
For i=0 to 255 do
S[i] = i
j=0
for i=0 to 255 do
j = ( j+S[i]+key[i mod L] )mod 256
Swap(S[i],S[j])
Return S
伪随机数生成算法:
Input: S盒
Output:生成的密钥流
i=0
j=0
while GeneratingOuput
I = (i+1) mod 256
j = (j+S[i]) mod 256
Swap(S[i],S[j])
Z = S[ (S[i]+S[j]) mod 256]
Output z
密钥key实际可用的长度最大为256字节,但典型的长度是40-128 bit。
Rc4的最初若干字节密钥流的非均匀分布
在密钥随机的前提下,如果密钥流是均匀的话,每个字节出现的概率应该是1/256=0.3906%,但从理论分析和实验结果来看,密钥流某些位置上的某些字节出现的概率要明显高于(或低于)其他字节,即偏移(biase)
RC4单字节偏移现象最初由Mantin and Shamir等人发现。他们指出密钥流的第二个字节,Z2=0的概率约为1/128,而不是1/256

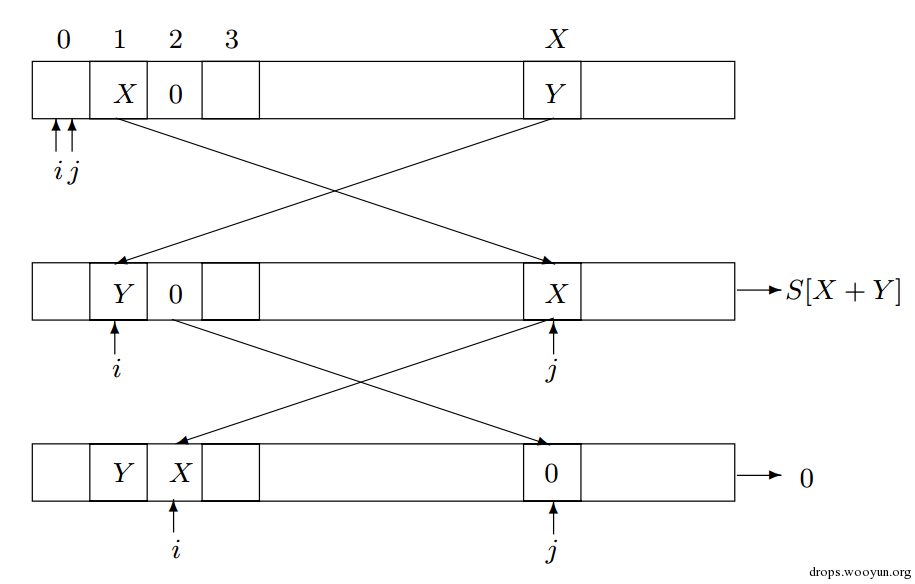
在S盒初始化结束,生成密钥流的过程中,假设S2=0,S1=X≠2,S[X]=Y,根据伪随机数生成算法,第一轮,S[X]和S1互换,生成的密钥字节是S[X+Y];第二轮,S2和S[X]互换,生成的密钥字节是S[X]=0,即Z2=0。
由条件概率公式,计算出z2=0的概率约为1/128
P[z2 = 0] = P[z2 = 0|S[2]= 0] * P[S[2]= 0]
+ P[z2 = 0|S[2] ≠ 0] * P[S[2] ≠ 0]
≈ 1*1/256 + 1/256*(1-1/256)
≈ 1/128
实验结果表明其他位置处的密钥字节也存在偏移现象。
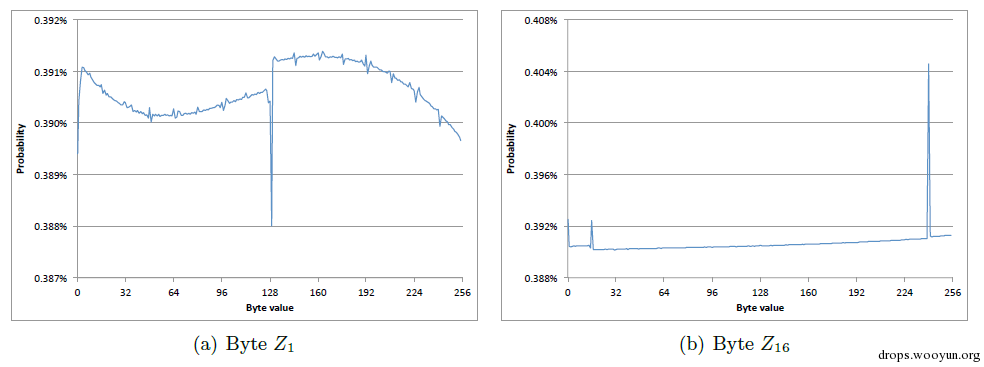
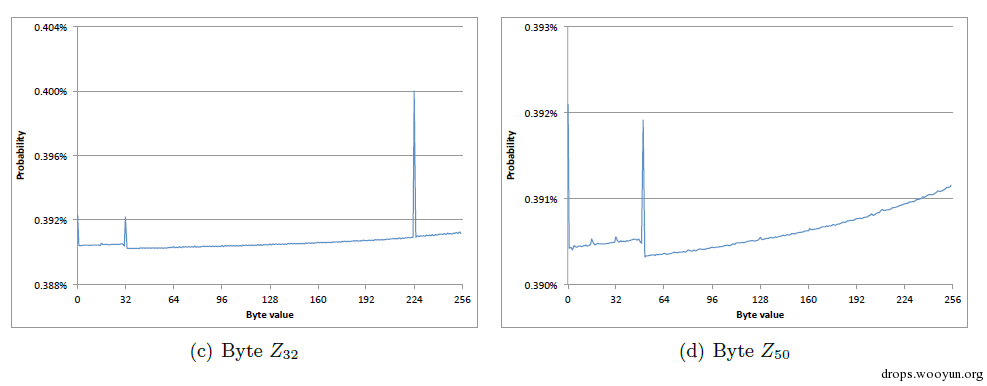
单字节偏移的局限性在于偏移现象只在初始的约256个字节出现。
多字节偏移又称long term biase,一些字节对出现的概率高于其他字节,会在密钥流中周期性的出现,最初由Fluhrer 和McGrew等人发现。
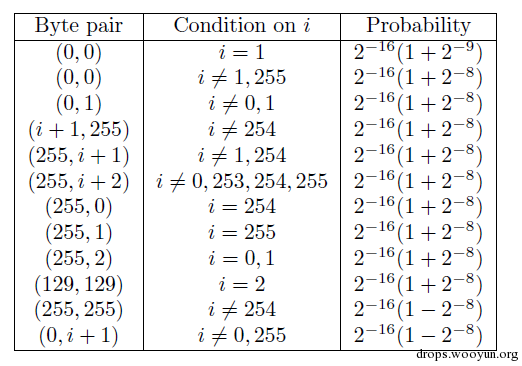
2015年Mathy Vanhoef及Frank Piessens发表了对RC4新的攻击方法,他们发现了新的偏移,只需要约9*2^27个密文就可以使cookie破解成功率达到94%,破解时间为75小时。这是第一个被证实可行的此类攻击。他们的论文《All Your Biases Belong to Us: Breaking RC4 in WPA-TKIP and TLS》发表在USENIX Security2015,并被评为Best Student Paper
学过概率与统计课程的同学应该对下面的题目有印象
“随机抛n次硬币,求恰好出现m次正面向上的概率”
这个概率符合二项分布,每次实验只有两种可能的结果。二项分布的名字来源于其概率公式符合二项展开的公式。
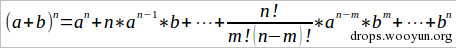
每次实验,两种结果出现的概率分别为a和b,重复实验n次,展开式中的每一项都是一个独立事件,如n*a^(n-1)*b表示第一种结果发生了n-1次,第二种结果发生了1次,这个现象发生的概率是n*a^(n-1)*b
将两种结果推广到更多的结果,就产生了多项分布。
“随机抛n次正方体骰子,点数1-6出现的次数分别为(x1,x2,x3,x4,x5,x6)的概率是多少,其中x1+x2+x3+x4+x5+x6=n”
更一般的情况是不规则的骰子。这种概率仍然符合多项展开公式

基于概率论的相关公式,我们就可以利用RC4密钥流中的偏移特性,对明文某一字节出现的概率进行计算,从而攻破RC4.
在预处理阶段,通过大量的实验,生成随机的key,统计密钥流中各字节出现的概率,类似求出前面多项展开式中的p1,p2
在获取密文阶段,通过一些手段,不断用RC4加密同样的明文,记录出现的密文.类似求出前面多项展开式中的n1,n2
最后,计算明文各个字节的概率,从概率较高的候选字节中恢复明文。

最后给出针对单字节偏移的明文概率估计的整体算法。

实验结果:当搜集的密文数为2^26时,前96个字节恢复的概率均超过50%;当密文数为2^32时,恢复的概率基本为100%。

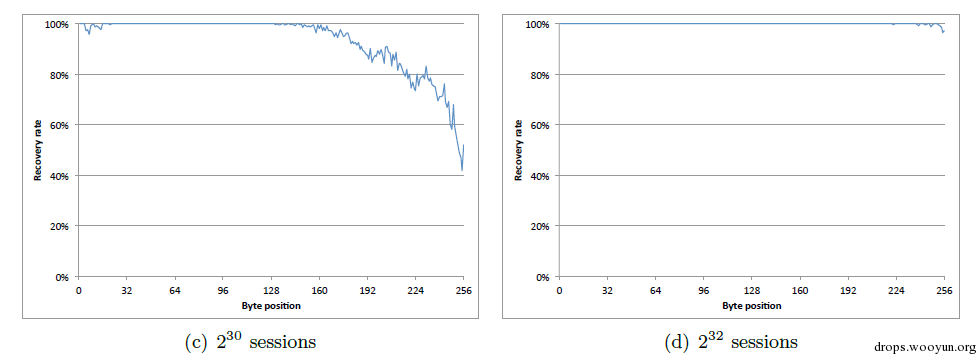
对于多字节偏移,还要用到更加复杂的概率公式,在此就不详细介绍了,但总体的思路还是一样的。此外,针对HTTP cookie,有简化运算的条件,如cookie字段总是以“Cookie:”开头,以换行符结尾,大部分cookie中的字符都是16进制字符。有兴趣的同学可以参考USENIX security2013年的论文《On the Security of RC4 in TLS and WPA》
或许有人会说,“既然密钥流初始的若干字节有偏移问题,抛弃那些字节不就可以继续用了么?”的确,RC4后来也出现了抛弃初始字节的版本RC4-drop N,但有问题的原始版本已经被大范围实现和部署,RC4的速度优势在当今硬件条件下也不是特别重要,因此TLS协议放弃RC4是一个方便、安全的选择。